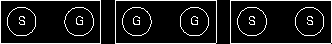Section 1.9 - Randomness

Like symmetry and independence, randomness is recognizable by the absence of contrary evidence. Concisely describing a pattern would be suitable contrary evidence. Randomness is best taken as a mathematical concept to avoid philosophical knots and physical antinomies. It’s like quantum mechanics: all outcomes are equally possible until the trial, when all possibilities collapse into the outcome (at which point randomness disappears). The concise pattern criterion seems to prohibit any kind of finitely defined random-number generator.

To some extent, randomness is relative: if you can’t figure out a pattern, then you should assume randomness, even though somebody else might be able to find a pattern. Relative randomness may be unpalatable, but it does allow a pragmatic justification for getting on with the task. Randomness can be interpreted as symmetry (identical probabilities, or uniformity), but symmetry can’t be interpreted as randomness. Sticking to symmetric sample spaces with independence helps sidestep semantic and philosophical problems with randomness. A random sample is actually an average over the sample space.

Example 1.9-1: A box has three drawers; one drawer holds two gold coins, one drawer holds two sliver coins, and the third draw holds a gold coin and a silver coin. Pick one of the drawers at random, and then from the chosen drawer pick one of the coins at random. The chosen coin is gold. What is the probability that the other coin is also gold?

First, notice the work “at random” is doing in the example. “At random” specifies that the choices being made are unbiased, or that any of the choices are equally likely to occur. That is, it’s providing justification for assuming that the resulting sample space, whatever it may be, is symmetric, making it possible to assign outcome probabilities.

It wasn’t necessary to use “at random” in die or card examples because tossing the die or cutting a well-shuffled deck was enough to justify symmetry.^?However, the finicky could state that “a die is tossed, producing a random result” or “a card is randomly cut from a well-shuffled deck” to avoid possibilities such as tossing a die by picking it up and putting it back down or forcing a card from a well-shuffled but nonetheless gaffed deck. “At random” could have been eliminated from the example by specifying, for example, that the chooser had no knowledge of the drawers’ contents, and was blindfolded while picking a coin (and that coins were indistinguishable other than visually).

Second, this example is a conditional-probability problem because ending up with a gold coin restricts the possible outcomes when choosing a drawer. If the example was “Pick a drawer at random. What is the probability it contains a gold coin?”, then choosing the drawer containing only silver coins is possible outcome. The gold-coin condition restricts the set of possible drawer choices, reducing the sample space.

However, the gold-coin condition also increases the sample space by distinguishing between the coins in the drawer: one of them is picked, and the other one isn’t.^?That is, the gold-coin condition adds another coordinate to the sample space. The original coordinate is the drawer chosen; the new coordinate is the coin chosen. Much in the same way the two sides of a coin are indistinguishable until the coin is flipped, the two coins in this example are indistinguishable until one is chosen.^?This may be a bad example because the two sides of a (normal) coin are distinguishable, even if the differences are ignored, while two identical coins are indistinguishable, even when the coins are distinguished. This is also the motivation for the suggestion to somehow assign each identical object a distinguishing mark that is irrelevant to the example but helpful in reasoning through the solution. The subscripts 1 and 2 are used below to distinguish otherwise identical coins.

A drawer can be represented by a pair of coins, and one of the coins in the pair—the first one, for example—can represent the chosen coin. The coins are represented by G or S for gold or silver, and by subscripts to distinguish between otherwise identical coins. The unconditional sample space is

chosen	G1	G2	S	G	S1	S2
unchosen	G2	G1	G	S	S2	S1

The gold-coin condition reduces the sample space to

chosen	G1	G2	G
unchosen	G2	G1	S

The sample-space size is 3; by symmetry (justified by randomness), each outcome has probability 1/3.

The solution to the example is at hand: two of the three possible outcomes have a gold coin remaining, for a probability of 2/3. The 2/3 probability may be a surprise because of the tendency to reason^?That is, this is how I first tried to solve the example. as follows:

There’re three drawers, but one of them contains only silver, leaving two drawers. The unpicked coin in one of the drawers is silver, the unpicked coin in the other drawer is gold. There’s a 50-50 chance of picking the extra gold coin.

This reasoning squeezes only half the juice out of the conditional orange; it recognizes the sample-space reduction implied by the gold coin, but ignores the sample-space expansion implied by choosing a particular coin. It matters when you choose between two identical coins (or any number of identical objects), not in terms of the coin picked, but in terms of the sample-space size.

Combine drawer picking with coin picking for an alternative way of thinking about the example. At random, lay out the six coins in a line on a table. Draw three boxes around consecutive coin pairs to represent the drawers.

Randomly picking a coin also corresponds to picking a drawer. The gold-coin condition eliminates three possible choices, which also eliminates one of the drawers, as described above.

Pick a gold coin. You have two opportunities to pick the drawer containing only gold, and one opportunity to pick the drawer containing gold and silver. Hence, 2/3.